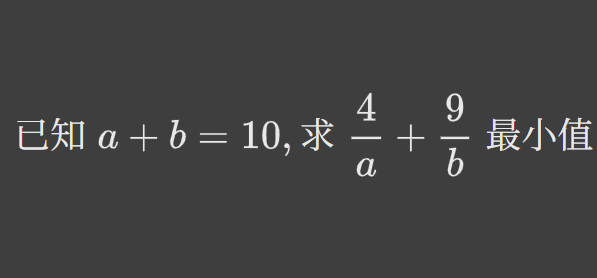
一道并不怎么经典的数学题——权方和不等式

权方和不等式： 对于两组非负实数 x_1, x_2, x_3,······, x_n 和 p_1, p_2, p_3,······, p_n \\ 有： \frac{x_{1}^{2}}{p_{1}} + \frac{x_{2}^{2}}{p_{2}} + \frac{x_{3}^{2}}{p_{3}} + ······ + \frac{x_{n}^{2}}{p_{n}} \ge \frac{(x_{1} + x_{2} + x_{3} + ······ +x_{n})^{2}}{p_{1} + p_{2} + p_{3} + ······ + p_{n}} \\ 带入可得： \\ \frac{2^{2}}{a} + \frac{3^{2}}{b} \ge \frac{(2 + 3)^{2}}{a + b} \\ 将 a + b = 10 带入可得 \\ a + b = 10,min(\frac{4}{a} + \frac{9}{b}) = \frac{5^{2}}{10} = 2.5 \\

权方和不等式： \\ 对于两组非负实数，x_1,x_2,x_3,······,x_n 和 p_1,p_2,p_3,······,p_n，有： \\ \frac{x_{1}^{2}}{p_{1}} + \frac{x_{2}^{2}}{p_{2}} + \frac{x_{3}^{2}}{p_{3}} + ······ + \frac{x_{n}^{2}}{p_{n}} \ge \frac{(x_{1} + x_{2} + x_{3} + ······ +x_{n})^{2}}{p_{1} + p_{2} + p_{3} + ······ + p_{n}} \\ 证明过程： \\ 设向量 a , b 分别为 a = (\frac{x_1}{\sqrt{p_1} },\frac{x_2}{\sqrt{p_2} },······,\frac{x_n}{\sqrt{p_n} } ), \overrightarrow(b) = (\sqrt{p_1},\sqrt{p_2},······,\sqrt{p_3} ) \\ 根据柯西不等式：(a·a)(b·b) \ge (a·b)^{2} \\ 计算点积和模长： \\ a·a = \frac{x_1^{2}}{p_1} + \frac{x_2^{2}}{p_2} + ······ + \frac{x_n^{2}}{p_n} \\ b·b = p_1 + p_2 + ······ + p_n \\ a·b = x_1 + x_2 + ······ + x_n \\ 带入柯西不等式： \\ (\frac{x_1^{2}}{p_1} + \frac{x_2^{2}}{p_2} + ······ + \frac{x_n^{2}}{p_n})(p_1 + p_2 + ······ + p_n) \ge (x_1 + x_2 + ······ + x_n)^{2} \\ 整理，得 \\ \frac{x_{1}^{2}}{p_{1}} + \frac{x_{2}^{2}}{p_{2}} + \frac{x_{3}^{2}}{p_{3}} + ······ + \frac{x_{n}^{2}}{p_{n}} \ge \frac{(x_{1} + x_{2} + x_{3} + ······ +x_{n})^{2}}{p_{1} + p_{2} + p_{3} + ······ + p_{n}}

首先我们知道，对于任何实数 a_i 和 b_i ，都有不等式： \\ \sum_{i=1}^{n} (a_i^{2} + b_i^{2}) \ge 0 \\ 然后我们可以构造一个二次函数： \\ f(x) = \sum_{i=1}^{n} (a_ix+b_i)^{2} \\ 展开亿下 \\ (\sum_{i=1}^{n} a_i^{2})x^{2}+2(\sum_{i=1}^{n} a_ib_i)x+\sum_{i=1}^{n} b_i^{2} \\ 由于这个关于 x 的二次函数对于所有的实数 x，都有 f(x) \ge 0 \\ 因此，这个二次函数的判别式必须小于或等于零 \\ 二次函数的判别式为：D = b^{2}-4ac，对于 f(x) \\ D = (2 \sum_{i=1}^{n} a_ib_i)^{2} - 4(\sum_{i=1}^{n} a_i^{2})(\sum_{i=1}^{n} b_i^{2}) \\ 因为 f(x) > 0 对所有 x 都成立，所以 D \le 0 \\ 带入判别式，得 \\ (2 \sum_{i=1}^{n} a_ib_i)^{2} - 4(\sum_{i=1}^{n} a_i^{2})(\sum_{i=1}^{n} b_i^{2}) \le 0 \\ 两边除以 4，得 \\ (\sum_{i=1}^{n} a_ib_i)^{2} - (\sum_{i=1}^{n} a_i^{2})(\sum_{i=1}^{n} b_i^{2}) \le 0 \\ 变形，得 \\ (\sum_{i=1}^{n} a_ib_i)^{2} \le (\sum_{i=1}^{n} a_i^{2})(\sum_{i=1}^{n} b_i^{2}) \\ 然后你看到得这一大坨就是柯西不等式： \\ (\sum_{i=1}^{n} a_ib_i)^{2} \le (\sum_{i=1}^{n} a_i^{2})(\sum_{i=1}^{n} b_i^{2}) \\ 也就是刚才的 (a·a)(b·b) \ge (a·b)^{2}