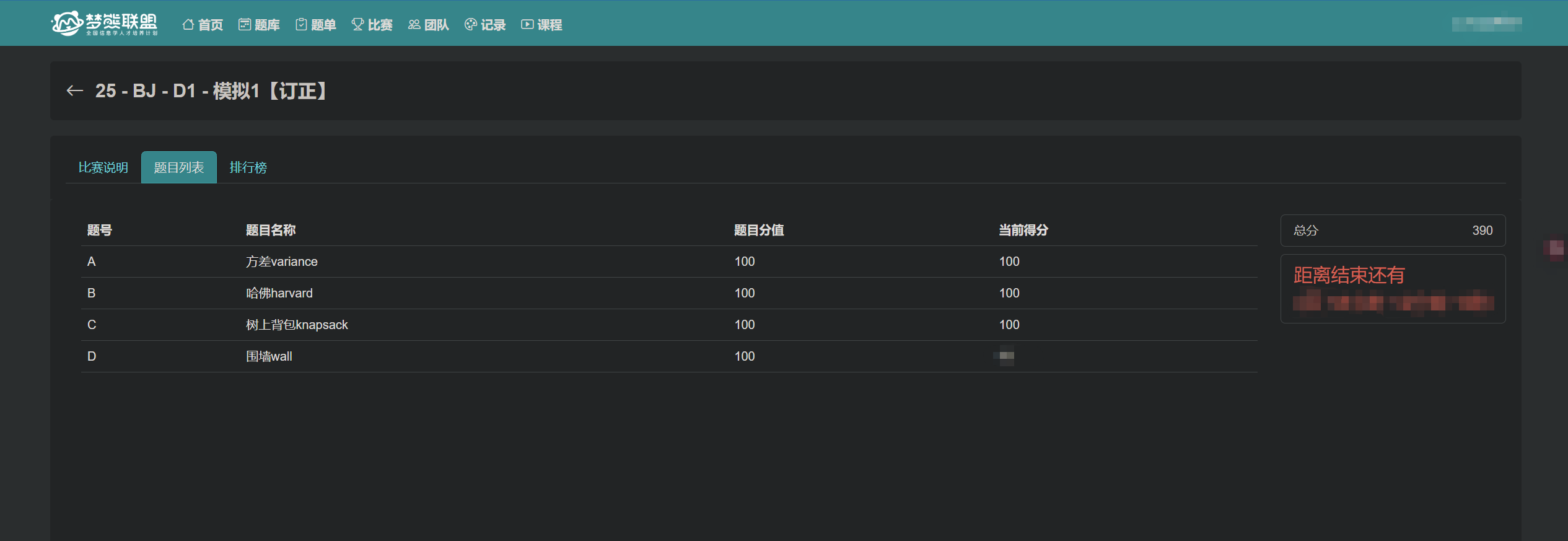
[梦熊] D班模拟赛-详细解析

题目及考察点

题目.pdf：

D 班模拟赛 contest20250719-MX.pdf

题目（补题）. 传送门：

邀请码找教练要去 (●'◡'●)

方差（variance.cpp）

• 考点：前缀和计算、平均数计算、方差计算、分数处理。

• 简要分析：主要考察对基本数学概念的理解和实现能力，需要正确计算前缀和、平均数和方差，并以分数形式输出结果。

哈佛（harvard.cpp）

• 考点：数位分离、数学运算、区间查询、前缀和优化。

• 简要分析：要求处理数字的各位非零数字乘积，并对区间内的所有数对的乘积和进行查询，重点在于如何高效地预处理和计算区间内的总和。

背包（knapsack.cpp）

• 考点：树的遍历、动态规划（背包问题）、状态转移、空间优化。

• 简要分析：该题是一个树形背包问题，需要在树的结构上进行动态规划，要求对树的遍历和背包算法的状态转移有深入理解，并能进行空间优化以适应题目中的数据规模。

围墙（wall.cpp）

• 考点：网格操作、区域判断、最大子矩阵计算、二维前缀和、离线处理。

• 简要分析：涉及网格的反转操作和围墙区域的判断，要求计算包含特定格子的围墙的最大面积，重点在于如何高效地处理网格的动态变化和区域判断。

题解

T1- 方差（variance.cpp）

这道题让我们输出每个前缀的和、平均数及方差，而且要求以最简分数输出（若非整数）。和、平均数很好算，重要的是方差。

方差的话暴力通分肯定是 WA 了（爆 long long），所以我们需要对公式进行转化（转为增量形式）：

这样再通分的话分母最多 n²

最后看 AC 正解：

#include<bits/stdc++.h>
#define ll long long//不必多说
using namespace std;
void print(ll a, ll b, char ch) {//本题特殊输出
    //有些比赛不让用 `std::__gcd()` ，所以最好自己写 `ll gcd(ll a, ll b) { return b ? gcd(b, a%b) : a; }` 也不费劲，背过就好了
    int c = __gcd(a, b);
    a /= c, b /= c;
    if (b == 1) {
        printf("%lld", a);
    }
    else {
        printf("%lld/%lld", a, b);
    }
    printf("%c", ch);
}
int main() {
    freopen("variance.in","r",stdin);//文件读写
    freopen("variance.out","w",stdout);
    ll n;
    scanf("%lld", &n);
    ll s1 = 0, s2 = 0;
    for (ll i = 1;i <= n;i++) {
        ll x;
        scanf("%lld", &x);
        s1 += x;s2 += x * x;
        print(s1, 1, ' ');
        print(s1, i, ' ');
        print(s2 * i - s1 * s1, i * i, '\n');//利用增量形式计算方差
    }
    return 0;
}

T2- 哈佛（harvard.cpp）

这道题暴力 O(qn²) 只能拿 60。但是你可以注意到 f(x) 的值域并不大，所以预计算前缀和即可，复杂度 O(n log A + V² log A + qV² )

AC 正解：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 10009;
int n, q, a[N], s[N];
unordered_map<int, int>V;
unordered_map<int, unordered_map<int, int> >G;
unordered_map<int, int>cnt[N];

int f(int x, int sum = 1) {
    while (x) {
        int a = x % 10;
        if (a != 0)sum *= a;
        x /= 10;
    }
    return sum;
}

void init() {
    for (int i = 1;i <= 1000;i++) {
        V[f(i)] = 1;
    }
    for (auto it = V.begin();it != V.end();it++) {
        for (auto itt = V.begin();itt != V.end();itt++) {
            G[it->first][itt->first] = __gcd(it->first, itt->first);
        }
    }
}

ll solve(int l, int r, ll sum = 0) {
    unordered_map<int, int>count = cnt[r];
    for (auto it = cnt[l - 1].begin(); it != cnt[l - 1].end(); ++it) {
        count[it->first] -= it->second;
    }

    for (auto it1 = count.begin(); it1 != count.end(); ++it1) {
        for (auto it2 = count.begin(); it2 != count.end(); ++it2) {
            sum += (ll)it1->second * it2->second * G[it1->first][it2->first];
        }
    }
    sum -= (s[r] - s[l - 1]);
    return sum / 2;
}

using namespace std;
int main() {
    freopen("harvard.in","r",stdin);
    freopen("harvard.out","w",stdout);
    init();

    cin >> n >> q;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
    }

    for (int i = 1; i <= n; ++i) {
        a[i] = f(a[i]);
        s[i] = s[i - 1] + a[i];
        cnt[i] = cnt[i - 1];
        cnt[i][a[i]]++;
    }
    for (int i = 0; i < q; ++i) {
        int l, r;
        cin >> l >> r;
        cout << solve(l, r) << endl;
    }

    return 0;
}

T3- 背包（knapsack.cpp）

这道题的题目跟正解没有任何关系，纯粹误导，正解是折半搜索 + 双游标拼接。预计算前 \sqrt(n) 个节点到根节点路径上的背包数组（从⽗节点增量转移） 后⼀半暴⼒枚举，然后剩余空间去预计算的数组⾥直接查（不⽤排序）

AC 正解：

#include<bits/stdc++.h>
#define L 100005
#define ll long long
int n,q,v[1<<18],w[1<<18];
ll f[512][L];
ll solve(int u, int l) {
    if (l <= 0) return 0;
    if (u < 512) return f[u][l];
    ll ans = solve(u/2,l);
    if (l>=w[u]) ans=std::max(ans, solve(u/2, l-w[u])+v[u]);
    return ans;
}
int main()  {
    scanf("%d",&n);
    for (int i=1; i<=n; i++) scanf("%d%d",v+i,w+i);
    for (int i=1; i<512; i++) {
        memcpy(f[i], f[i/2], sizeof(f[i]));
        for (int j=L; j>=w[i]; --j)
            f[i][j]=std::max(f[i][j-w[i]]+v[i],f[i][j]);
    }
    scanf("%d",&q);
    for (int u,l; q--; printf("%lld\n", solve(u,l)))
        scanf("%d%d", &u, &l);
    return 0;
}

T4- 围墙（wall.cpp）

敬请期待 懒得写以后再写